Ubungsaufgaben

[Weiter] [Zurück] [Zurück (Ende)] [Ende] [Hoch]

1.8 Übungsaufgaben

Frage 1: Nennen und erklären Sie kurz die vier Zinseffekte.

Antwort Frage 1

Liquiditätseffekt (Keynes-Effekt): Beschreibt den Zusammenhang zwischen Zinssatz und Angebot bzw. Nachfrage der Geldmenge. Erhöht ich das Geldangebot, so sinkt der Preis des Geldes (Zins), c.p.

Preisniveaueffekt (Fisher-Effekt): Der Nominalzins steigt 1 zu 1 mit der (erwarteten Inflationsrate.

Unsicherheitseffekt (Friedman-Effekt): Risikoaverse Kapitalgeber verlangen eine Risikoprämie für die mit geldpolitischen Maßnahmen verbundenen Unsicherheiten. Je größer die Unsicherheit, desto größer die Risikoprämie und dadurch der Zins.

Einkommenseffekt (Wicksel-Effekt): Sinkt der Nominalzins, dann können Unternehmen aufgrund geringerer Kosten mehr Kredite aufnehmen und so mehr investieren, wodurch das BIP/Einkommen steigt.

Frage 2: Zeigen Sie graphisch den (i) Liquiditätseffekt, (ii) Preisniveaueffekt und (iii) Unsicherheitseffekt.

Antwort Frage 2

Frage 3: Erklären Sie die klassische Dichotomie

Antwort Frage 3

Die klassische Dichotomie beschreibt, dass die monetäre Wirtschaft von der Realwirtschaft abgetrennt ist. Geldpolitische Maßnahmen führen lediglich zu einer Änderung des Preisniveaus, während realwirtschaftliche Variablen nicht beeinflusst werden (Neutralität des Geldes).

Frage 4: Geben Sie die IS-Gleichung formal wieder und erläutern Sie die Zusammenhänge der exogenen Variablen auf die endogene Variable.

Antwort Frage 4

IS-Gleichung: Y = C(Y-T)+I(Y,I)+G

Einfluss der exogenen Variablen auf die endogene Variable:
G ↑ → Y ↑
I ↑ → Y ↑
C ↑ → Y ↑
Y ↑ → I ↑ → Y ↑
Y ↑ → (Y-T) ↑ → C ↑ → Y ↑
T ↑ → (Y-T) ↓ → C ↓ → Y ↓

Frage 5: Formal lässt sich der Konsum C auch als Keynesianische Konsumfunktion darstellen: C=c0 + c1 * (Y-T), wobei c0 eine Konstante ist, welche lebensnotwendige Konsumausgaben wiederspiegelt. c1 ist die marginale Konsumneigung und beschreibt den zusätzlichen Konszm, wenn das verfügbare Einkommen um 1 Einheit steigt.

(a) Berechnen Sie das BIB, gegeben folgender Annahmen: c = 1500, I = 500, G = 250.

Antwort Frage 5 (a)

Y = C + I + G = 1500 + 500 + 250 = 2250

(b) Aufgrund von gestiegenen Inflationserwartungen erhöht die Zentralbank den Leitzins um5%. Wie wirkt sich die Zinserhöhung auf das BIP aus? Begründen Sie kurz Ihre Antwort.

Antwort Frage 5 (b)

Der Zinsanstieg besitzt einen negativen Einfluss auf das BIP. Die höheren Zinsen führen zu einem Investitionsrückgang, wodurch wiederum das BIP sinkt.
i ↑→ I↓→ Y↓
i ↑→ C↓→ Y↓

(c) Um Schulen und Universitäten zu modernisieren, beschließt der Staat 50 Einheiten zusätzlich in Schulen und Universitäten zu investieren. Verglichen zu (a), welche Variable verändert sich durch diese Maßnahmen? Berechnen Sie außerdem das neue BIP.

Antwort Frage 5 (c)

Die Staatsausgaben verändern sich: G steigt um 50 Einheiten, d.h. G' = 300.
Y = C + I + G' = 2300.

(d) Angenommen die Lebenserhaltungskosten betragen in Deutschland 1000 EUR. Für jeden zusätzlichen verfügbaren Euro steigt der Konsum um 25%. Nehmen Sie an, der Staatshaushalt in Deutschland ist ausgeglichen. Berechnen Sie Einkommen und Konsum anhand der Werten von (c).

Antwort Frage 5 (d)

C = c0 + c1 * (Y - T) = 10000 + 0.25 * (2300 - 300) = 1500
Y = C + I + G = 1500 + 500 + 300 = 2000

Frage 6: Durch die Änderung welcher Variablen verschiebt sich die IS-Kurve? Durch die Änderung welcher Variablen kommt es zu einer Bewegung entlang der IS-Kurve? Es können mehr als eine Antwort richtig sein.

(i) Verschiebung der IS-Kurve

(ii) Bewegung entlang der IS-Kurve

Frage 7: Definieren Sie die IS-Kurve.

Antwort Frage 7

Die IS-Kurve bildet alle (Y, i)-Kombinationen ab, in denen sich der Gütermarkt im Gleichgewicht befindet.

Frage 8: Aufgrund schlechter wirtschaftlicher Prognose möchte die Politik die Konjunktur durch höhere Staatsausgaben unterstützen. Um die höheren Ausgaben zur finanzieren sollen die Steuern um den gleichen Betrag angehoben werden. Ist die politische Maßnahme zu befürworten? Nehmen Sie an, der Staatshaushalt ist ausgeglichen. Begründen Sie Ihre Antwort.

Antwort Frage 8

Ausgeglichener Staatshaushalt bedeutet: T = G bzw. ΔT = ΔG
Y = c₀ + c₁(Y - T) + I + G
Y = c₀ + c₁Y - c₁T + I + G
(1 - c₁)Y = c₀ + I + G - c₁T
Y = ¹⁄_{(1 - c₁)} (c₀ + I + G) - ^c₁⁄_{(1 - c₁)} T .

Da c₁ > 1 gilt, dass ¹⁄_{(1 - c₁)} > ^c₁⁄_{(1 - c₁)}. Dadurch hat eine Änderung in G einen stärkeren Einfluss auf das Y als eine Änderung in T. Solange also c₁ > 1 und ΔT = ΔG erfüllt ist, führen höhere Staatsausgaben finanziert durch höhere Steueren zu einem höheren Einkommen. Eine solche politische Maßnahme ist zu befürworten.

Frage 9: Definieren Sie die LM-Kurve.

Antwort Frage 9

Die LM-Kurve bildet alle (Y,i)-Kombinationen ab, in denen der Geld- und Finanzmarkt sich im Gleichgewicht befindet.

Frage 10: Geben SIe die LM-Kurve formal wieder und erläutern Sie was passiert, wenn sich die Basisvariablen ändern?.

Antwort Frage 10

M=M^S=M^D=YPL(i)⇔YL(i)

Y ↑→ M^D ↑→ LM ↑→ i ↑

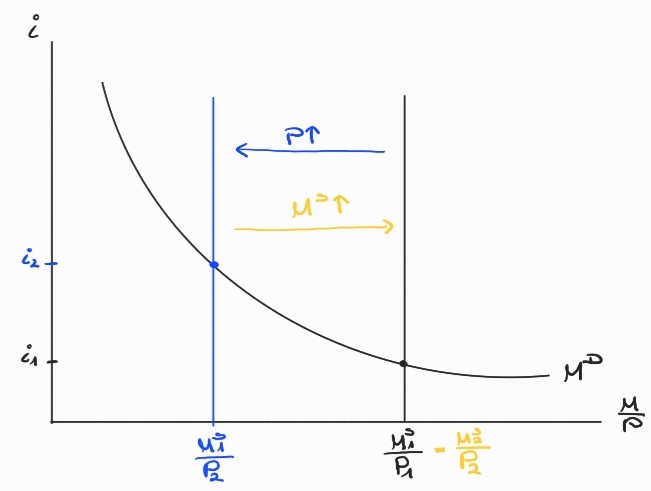
P ↑→ M/P ↑

i ↑→ M^D ↑

Frage 11: Im Zuge eines Krieges wird Rohöl immer teurer, wodurch das Preisniveau steigt. Wie kann die Zentralbank reagieren, um das Zinsniveau konstant zu halten, c.p. ? Erklären Sie Ihre Antwort graphisch und verbal.

Antwort Frage 11

Durch das höhere Preisniveau sinkt die reale Geldmenge (reales Geldangebot), c.p.: P ↑→ M^S/P ↓. Würde die Zentralbank nicht intervenieren, würde der Zinssatz als Folge steigen. Um dies zu verhindern, muss die Zentralbank das nominale Geldangebot (M^S) soweit erhöhen, dass die reale Geldmenge konstant bleibt und dadurch auch der Zinssatz.

Frage 12: Durch die Änderung welcher Variablen kommt es zu einer Verschiebung bzw. Bewegung entlang der LM-Kurve?

(i) Verschiebung der LM-Kurve

(ii) Bewegung entlang der LM-Kurve

Frage 13: Erklären Sie expansive und kontraktive Fiskalpolitik.

Antwort Frage 13

Als Fiskalpolitik wird die staatliche Einflussnahme auf die Konjunktur bezeichnet, indem der Staat seine Ausgaben und/oder Steuereinnahmen verändert.

Expansive Fiskalpolitik: Ausweitung des Staatsbudgets, um Konjunkturanzukurbeln (G ↑ und/oder T↓).

Kontraktive (oder restriktive) Fiskalpolitik: Ausweitung des Staatsbudgets, um Konjunkturanzukurbeln (G ↓ und/oder T↑).

Frage 14: Zeigen Sie graphisch die Auswirkungen im ISLM-Modell einer (i) expansiven und (ii) restriktiven Fiskalpolitik und beschreiben Sie diese Verbal.

Antwort Frage 14

Expansive Fiskalpolitik: G ↑ und/oder T ↓→ IS ↑→ Y ↑→ M^D ↑→ i↑
Kontraktive (oder restriktive) Fiskalpolitik: G ↓ und/oder T↑→ IS ↓→ Y ↓→ M^D↓→ i↓

Frage 15: Als Multiplikator versteht die VWL das Verhältnis der Änderung einer endogenen Variablen zur Änderung einer exogenen Variablen. Zeigen Sie formal den Multiplikatoreffekt einer expansiven Fiskalpolitik.
TIP: Beachten Sie hierfür die keynsianische Konsumfunktion.

Antwort Frage 15

\[Y = c_0 + c_1 (Y - T) + I + G = c_0 + c_1 Y - c_1 T + I + G\] \[(1 - c_1)Y = c_0 - c_1 T + I + G\] \[Y = \frac{1}{1 - c_1}(c_0 - c_1 T + I + G)\] \[\frac{\delta Y}{\delta G} = \frac{1}{1 - c_1}\]

Der Multiplikatoreffekt einer expansiven Fiskalpolitik (z.B. G↑): \( \Delta G \cdot \frac{1}{1 - c_1} \)

Frage 16: Erklären Sie expansive und restriktive Geldpolitik.

Antwort Frage 16

Geldpolitik bezeichnet die Einflussnahme der Zentralbank (bzw. geldpolitischen Authorität) auf die Konjunktur durch die Veränderung der (nominalen) Geldmenge.

Expansive Geldpolitik: Erhöhung der Geldmenge; Zentralbank kauft Anleihen/Wertpapiere durch Offenmarktgeschäfte.

Restriktive Geldpolitik: Reduzierung der Geldmenge; Zentralbank verkauft Anleihen/Wertpapiere durch Offenmarktgeschäfte.

Frage 17: Beschreiben Sie verbal die Auswirkungen einer expansiven Geldpolitik.

Antwort Frage 17

Durch die Erhöhung des (nominalen) Geldangebots ist mehr Geld im Umlauf als zum ursprünglichen Gleichgewichtszins nachgefragt wird. Folglich sinkt der Preis des Geldes (d.h. der Zinssatz). Die niedrigeren Zinsen stimulieren Investitionen, wodurch es zu einem Einkommensanstieg kommt.
Expansive Geldpolitik verschiebt die LM-Kurve nach rechts: M^S ↑→ i ↓→ I ↑→ Y ↑

Frage 18: Gegeben sind die folgenden Nachfragefunktionen für Konsum, Investition und Geld: C = 80 + 0.8(Y - T), I = 150 - 1000i, M/P = 0.2Y - 1000i. Das Preisniveau sei auf P = 1 fixiert.

(a) Bestimmen Sie die IS- und LM-Kurve. Die Staatsausgaben betragen G = 100 und das Staatsbudget ist ausgeglichen. Das reale Geldangebot beträgt M/P = 50.

Antwort Frage 18 (a)

IS-Kurve: \( Y = C + I + G \)

\( Y = 80 + 0.8(Y - 100) + 150 - 1000i - 100 = 250 + 0.8Y - 1000i \)

\( 0.2Y = 250 - 1000i \)

\( Y = 1250 - 5000i \)

LM-Kurve: \( \frac{M}{P} = YL(i) \)

\( 50 = 0.2Y - 1000i \)

\( Y = 250 + 5000i \)

(b) Berechnen Sie den Zinssatz bei dem sich der Geld- und Gütermarkt im Gleichgewicht befindet.

Antwort Frage 18 (b)

Schritt 1: Um den gleichgewichtigen Zinssatz zu bestimmen, muss die IS- und LM-Kurve gleichgesetzt werden:

\( 1250 - 5000i = 250 + 5000i \)

\( 1000 = 10000i \)

\( i = 0.1 = 10\% \)

Schritt 2: Nun kann der Zinssatz in die IS- oder LM-Kurve eingesetzt werden, um das Gleichgewichtseinkommen bei gegeben Zinssatz zu bestimmen.

Einkommen: \( Y = 250 + 5000 \times 0.1 = 750 \)

Verfügbares Einkommen: \( Y - T = 750 - 100 = 650 \)

Schritt 3: \( Y - T = 650 \) in Konsumfunktion einsetzen, um den Konsum im Gleichgewicht zu bestimmen und Zinssatz in Investitionsfunktion einsetzen, um die Höhe der Investition im Gleichgewicht zu bestimmen.

\( C = 80 + 0.8 \times 650 = 600 \)

\( I = 150 - 1000 \times 0.1 = 50 \)

(c) Nehmen Sie an, der Staat erhöht seine Ausgaben auf \( G = 250 \), c.p., wobei er die Differenz mit Krediten finanziert. Bestimmen Sie die neuen Gleichgewichtswerte für Zins, (verfügbares) Einkommen, Konsum und Investitionen.

Antwort Frage 18 (c)

IS-Kurve:

\( Y = 80 + 0.8(Y - 100) + 150 - 1000i + 250 = 400 + 0.8Y - 1000i \)

\( 0.2Y = 400 - 1000i \)

\( Y = 2000 - 5000i \)

LM-Kurve:

\( Y = 250 + 5000i \)

Berechnung der Gleichgewichtswerte:

\( 2000 - 5000i = 250 + 5000i \)

\( 10000i = 1750 \)

\( i = 17.5\% \)

Y = 250 + 5000 \times 0.175 = 1125

Y - T = 1125 - 100 = 1025

C = 80 + 0.8 \times 1025 = 900

Investitionen und Ersparnisse:

I = 150 - 1000 \times 0.175 = -25

Negative Investitionen bedeuten Ersparnisse. Aus \( I = S - (G - T) \) lassen sich die privaten Ersparnisse berechnen.

-25 = S - (250 - 100)

S = 125

Die Erhöhung der Staatsausgaben, finanziert durch Kredite, verdrängen private Investitionen (\( I \)) vom Markt und die Ersparnisse (\( S \)) steigen. Diesen Effekt bezeichnet man als „Crowding-Out“.

Frage 19: Betrachten Sie folgende Volkswirtschaft:
\( C = 200 + 0.6(Y - T) \)
\( I = 200 + 0.2Y - 150i \)
\( \frac{M}{P} = Y - 15000 \)
\( G = T = 100 \)
\( M = 1000 \)
\( P = 2 \)

(a) Berechnen Sie die Gleichgewichtswerte für Y, i, I und C.

Antwort Frage 19 (a)

IS-LM Modell

IS-Kurve

\( Y = 200 + 0.6(Y - 100) + 200 + 0.2Y - 150i + 100 \)
\( 0.2Y = 440 - 150i \)
\( Y = 2200 - 750i \)

LM-Kurve

\( \frac{1000}{2} = Y - 15000i \)
\( Y = 500 + 15000i \)

IS = LM

\( 2200 - 750i = 500 + 15000i \)
\( 15750i = 1700 \)
\( i = 0.1079 \) (10.79%)
\( Y = 500 + 15000 \times 0.1079 = 2118.5 \)
\( I = 200 + 0.2 \times 2118.5 - 150 \times 0.1079 = 607.52 \)
\( C = 200 + 0.6(2118.5 - 100) = 1411.1 \)

(b) Nehmen Sie an, dass sich das Preisniveau plötzlich verdoppelt. Als Folge des Preisniveauanstiegs beschließt die Zentralbank die Geldmenge um 600 Einheiten zu erhöhen. Berechnen Sie die neuen Gleichgewichtswerte. Konnte die Zentralbank den Preisanstieg durch ihre expansive Geldpolitik ausgleichen?.

Antwort Frage 19 (b)

Neue LM-Kurve

\( \frac{1600}{4} = Y - 15000i \)
\( Y = 400 - 15000i \)

Neues Gleichgewicht

\( 2200 - 750i = 400 - 15000i \)
\( 15750i = 1800 \)
\( i = 0.1143 \) (11.43%)
\( Y = 2114.5 \)
\( I = 605.75 \)
\( C = 1408.7 \)

Frage 20: Zeigen Sie graphisch wie sich durch Koordination von Fiskal- und Geldpolitik das BIP erhöhen lässt, aber der Zins konstant gehalten werden kann. Begründen Sie Ihre Antwort verbal.

Antwort Frage 20

Durch expansive Fiskalpolitik kann der Staat die Konsumnachfrage erhöhen. Durch niedrigere Steuern erhöht sich das verfügbare Einkommen und die Geldnachfrage steigt. Die höhere Geldnachfrage führt zu einem Anstieg des Zinssatzes. Um den Zinssatz konstant zu halten, muss die Zentralbank das (nominale) Geldangebot erhöhen, sodass der Zinssatz wieder sinkt. Die Zentralbank verfolgt also eine expansive geldpolitische Maßnahme, um den Zinssatz wieder zu drücken. Diese expansive Geldpolitik kurbelt die Wirtschaft zusätzlich an, während der Zinssatz unverändert bleibt.

Expansive Fiskalpolitik: T ↓ und/oder G ↑→ IS ↑→ i ↑ Y ↑
Expansive Geldpolitik: M^S ↑→ LM ↓→ i ↓ Y ↑

Frage 21: Um Staatsschulden abzubauen erhöht der Staat seine Steuern. Die Zentralbank habe als oberstes Ziel die Wirtschaftsleistung im Land konstant zu halten. Zeigen Sie anhand des ISLM-Modells graphisch die Auswirkungen.

Antwort Frage 21

Restriktive Fiskalpolitik: T ↑ und/oder G ↓→ IS ↓→ i ↓ Y ↓
Expansive Geldpolitik: M^S ↑→ LM ↓→ i ↓ Y ↑

Antwort Frage 25

1. M ^S ↑→ M/P ↑→ r ↓→ Y ↑
Expansive Geldpolitik bedeutet die Ausweitung des nominalen Geldangebots, wodurch die reale Geldmenge steigt. Die LM-Kurve verschient sich folglich nach rechts und der reale Zinssatz sinkt und das Einkommen steigt.

2. r ↓→ r ^e ↓→ I ↑→ Y ↑
Aufgrund des niedrigeren Realzinses, passen sie Konsumenten ihre realen Zinserwartungen entsprechend nach unten an. Dadurch kommt es zu einem sog. "Zweitrundeneffekt": Durch die niedrigeren realen Zinserwartungen, erhöhen die Konsumenten die Investitionen und das Einkommen steigt. Die IS-Kurve verschiebt sich dadurch nach rechts. Beachte, dass die Auswirkungen auf die IS-Kurve allerdings gering ausfallen.
Unterschied zum ISLM-Modell ohne Erwartungen:

Betrachtung des realen Zinssatzes (nicht nominaler Zins)
Steilerer Verlauf der IS-Kurve aufgrund realen Zinserwartungen
IS-Kurve verschiebt sich aufgrund von Änderungen des erwarteten Realzinsen (Zweitrundeneffekt)

Antwort Frage 27 (a)

Aufgrund der Nullzinsgrenze kann der Zinssatz nicht (weit) unter Null fallen. Aus diesem Grund verläuft die LM-Kurve horizontal, sobald der Zinssatz Null erreicht wird. Graphisch spricht man von der Liquiditätsfalle, wenn die sich die IS- und LM-Kurve bei der Nullzinsgrenze schneiden. Eine Liquiditätsfalle tritt ein, wenn

aufgrund einer Wirtschaftskrise die IS-Kurve ausreichend weit nach links verschoben wird (z. B. Konjunktureinbruch, Sparprogramme, des Staates, Nachlassen der Konsumnachfrage, Austeritätspolitik, usw.).
aufgrund von expansiver Geldpolitik die LM-Kurve ausreichend weit nach rechts verschoben wird (z. B. Verhindern einer Wirtschaftskrise).

Im Zustand einer Liquiditätsfalle führt eine Ausweitung der Geldmenge zu keiner Zinssenkung, d.h. die Geldnachfrage ist unendlich zinselastisch und konventionelle (expansive) Geldpolitik ist wirkungslos.

Als Beispiel der Liquiditätsfalle kann man den Euroraum ab der Finanzkrise 2008/09 nennen. Aufgrund einer drohenden Rezession weitete die EZB die Geldmenge massiv aus, wodurch der Leitzins (Hauptrefinanzierungszins) von 4% (Juli 2008) auf 0% (März 2016). Der Leitzins blieb bis Juli 2022 bei 0%. Andere Zinsen sind in diesem Zeitraum teilweise sogar Unter die Nullzinsgrenze gefallen. Als aufgrund der Nullzinsgrenze konventionelle Geldpolitik (Ausweitung der Geldmenge durch Offenmarktgeschäfte) wirkungslos wurde, musste die EZB auf unkoventionielle geldpolitische Maßnahmen zurückgreifen, um eine Rezession zu verhindern. Durch begann die EZB das sog. "Anleihenkaufprogramm", womit die EZB Staatsanleihen kaufte, um so den langfristigen Zinssatz zu drücken. Allerdings ist zu erwähnen, dass wirksam dieser Maßnahmen in der Wissenschaft umstritten ist.

Antwort Frage 27 (b)

Liquidity Easing (LE): bezeichnet die Änderung von Zentralbankrichtlinien, damit Banken mehr Geld erhalten und somit die Wirtschaft stabilisiert oder durch vermehrte Kreditvergabe stimuliert wird. Unter LE fällt
- Akzeptanz von Sicherheiten mit niedrigerem Rating.
- unbefristete/langfristige Bereitstellung von Liquidität von Seiten der Zentralbank (Refinanzierungsoperationen mit mehrjähriger Laufzeit)
Credit Easing (CE): Zentralbanken treten als Konsumenten bestimmter Märkte auf (i.d.R. Kauf von Wertpapieren), um diese zu stabilisieren. Durch den Kauf von bestimmten Wertpapieren kann die Zentralbank verhindern, dass es zu Kurseinbrüche kommt, wodurch die folgenden Bilanzverschlechterungen der Banken zu Bankinsolvenzen führen.
Quantitative Easing (QE): Zentralbanken kaufen Staatsanleihen, um die Geldmenge zu erhöhen. Diese Maßnahme ergriff bspw. die EZB nach der Finanz- und Eurokrise, nachdem der kurfristige Zinssatz die Nullzinsgrenze erreichte. Durch den Kauf von Staatsanleihen mit mehrjähriger Laufzeit soll der langfristige Zinsatz reduziert werden. So sollen Investitionsentscheidungen und Konjunktur langfristig angekurbelt werden.